Sada, mirni, prelazimo na razmatranje divne granice.
izgleda kao .

Umjesto varijable x mogu biti prisutne različite funkcije, glavna stvar je da teže 0.

Moramo izračunati granicu

Kao što vidite, ova granica je vrlo slična prvoj izuzetnoj, ali to nije sasvim tačno. Općenito, ako primijetite grijeh u granici, onda biste trebali odmah razmisliti o tome da li je moguće koristiti prvu izvanrednu granicu.

Prema našem pravilu br. 1, zamjenjujemo nulu za x:

Dobijamo neizvjesnost.

Pokušajmo sada samostalno organizirati prvu izvanrednu granicu. Da bismo to učinili, izvršit ćemo jednostavnu kombinaciju:

Dakle, raspoređujemo brojilac i imenilac tako da se ističe 7x. Poznata izuzetna granica se već pojavila. Preporučljivo je to istaknuti prilikom odlučivanja:

Zamijenimo rješenje prvog izvanrednog primjera i dobijemo:

Pojednostavite razlomak:

Odgovor: 7/3.

Kao što vidite, sve je vrlo jednostavno.

Ima formu , gdje je e = 2,718281828… iracionalan broj.

Umjesto varijable x, mogu biti prisutne različite funkcije, glavna stvar je da teže .

Moramo izračunati granicu

Ovdje vidimo prisustvo stepena ispod znaka granice, što znači da se može primijeniti druga izuzetna granica.

Kao i uvek, koristićemo pravilo broj 1 - zamena umesto x:

Može se vidjeti da je za x osnova stepena , a eksponent 4x > , tj. dobijamo nesigurnost oblika:

Iskoristimo drugu divnu granicu da otkrijemo svoju neizvjesnost, ali prvo je moramo organizirati. Kao što vidite, potrebno je postići prisustvo u indikatoru, za šta podižemo bazu na stepen od 3x, a istovremeno na stepen od 1/3x, kako se izraz ne bi promijenio:

Ne zaboravite istaknuti naše divno ograničenje:

Ovo je stvarno divne granice!
Ako imate bilo kakvih pitanja o prva i druga divna granica slobodno ih pitajte u komentarima.
Svima ćemo odgovoriti u najkraćem mogućem roku.

Takođe možete raditi sa nastavnikom na ovoj temi.
Sa zadovoljstvom Vam možemo ponuditi usluge odabira kvalifikovanog tutora u Vašem gradu. Naši partneri će u najkraćem roku odabrati dobrog učitelja za vas po povoljnim uslovima za vas.

Nemate dovoljno informacija? - Možeš !

Možete pisati matematičke proračune u notes. Mnogo je prijatnije pisati u pojedinačne sveske sa logotipom (http://www.blocnot.ru).

Postoji nekoliko divnih granica, ali najpoznatije su prva i druga divna granica. Izvanredna stvar u vezi sa ovim ograničenjima je da se široko koriste i da se mogu koristiti za pronalaženje drugih ograničenja na koja se susreću u brojnim problemima. To je ono što ćemo raditi u praktičnom dijelu ove lekcije. Da bismo riješili probleme svođenjem na prvu ili drugu izuzetnu granicu, nije potrebno otkrivati ​​nesigurnosti sadržane u njima, budući da su vrijednosti ovih granica odavno zaključili veliki matematičari.

Prva izuzetna granica naziva se granica omjera sinusa beskonačno malog luka i istog luka, izražena u radijanskoj mjeri:

Pređimo na rješavanje problema na prvoj izuzetnoj granici. Napomena: ako je trigonometrijska funkcija ispod graničnog znaka, to je gotovo siguran znak da se ovaj izraz može svesti na prvu izvanrednu granicu.

Primjer 1 Pronađite granicu.

Rješenje. Umjesto toga x nula dovodi do neizvjesnosti:

.

Imenilac je sinus, stoga se izraz može svesti na prvu izuzetnu granicu. Započnimo transformaciju:

.

U nazivniku - sinus od tri x, au brojniku je samo jedan x, što znači da trebate dobiti tri x u brojiocu. Za što? Predstaviti 3 x = a i dobiti izraz.

I dolazimo do varijacije prve izvanredne granice:

jer nije bitno koje je slovo (varijabla) u ovoj formuli umjesto x.

Pomnožimo x sa tri i odmah podijelimo:

.

U skladu sa navedenom prvom značajnom granicom, zamjenjujemo frakcijski izraz:

Sada konačno možemo riješiti ovu granicu:

.

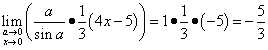Primjer 2 Pronađite granicu.

Rješenje. Direktna zamjena opet dovodi do nesigurnosti "nulte podjele na nulu":

.

Da bismo dobili prvu izuzetnu granicu, potrebno je da x ispod predznaka sinusa u brojiocu i samo x u nazivniku budu sa istim koeficijentom. Neka je ovaj koeficijent jednak 2. Da biste to učinili, zamislite trenutni koeficijent na x kao dolje, izvodeći radnje sa razlomcima, dobijamo:

.

Primjer 3 Pronađite granicu.

Rješenje. Prilikom zamjene opet dobivamo nesigurnost "nula podijeljena sa nulom":

.

Verovatno već razumete da iz originalnog izraza možete dobiti prvu divnu granicu pomnoženu sa prvom divnom granicom. Da bismo to učinili, razlažemo kvadrate x u brojiocu i sinus u nazivniku na iste faktore, a da bismo dobili iste koeficijente za x i sinus, podijelimo x u brojiocu sa 3 i odmah pomnožimo sa 3. Dobijamo:

.

Primjer 4 Pronađite granicu.

Rješenje. Opet dobijamo nesigurnost "nula podeljena sa nulom":

.

Možemo dobiti omjer prve dvije izuzetne granice. Podijelimo i brojilac i imenilac sa x. Zatim, da bi se koeficijenti na sinusima i na x poklopili, gornji x pomnožimo sa 2 i odmah podijelimo sa 2, a donji x pomnožimo sa 3 i odmah podijelimo sa 3. Dobijamo:

Primjer 5 Pronađite granicu.

Rješenje. I opet, nesigurnost "nula podijeljena sa nulom":

Iz trigonometrije se sjećamo da je tangenta omjer sinusa i kosinusa, a kosinus nule jednak je jedan. Pravimo transformacije i dobijamo:

.

Primjer 6 Pronađite granicu.

Rješenje. Trigonometrijska funkcija pod znakom granice opet sugerira ideju primjene prve izvanredne granice. Predstavljamo ga kao omjer sinusa i kosinusa.

Prva izuzetna granica izgleda ovako: lim x → 0 sin x x = 1 .

U praktičnim primjerima često se susreću modifikacije prve značajne granice: lim x → 0 sin k · x k · x = 1 , gdje je k neki koeficijent.

Objasnimo: lim x → 0 sin (k x) k x = prazno t = k x i iz x → 0 slijedi t → 0 = lim t → 0 sin (t) t = 1 .

Posljedice prve izuzetne granice:

1. lim x → 0 x sin x = lim x → 0 = 1 sin x x = 1 1 = 1

1. lim x → 0 k x sin k x = lim x → 0 1 sin (k x) k x = 1 1 = 1

Ove posljedice je prilično lako dokazati primjenom L'Hospitalovog pravila ili promjenom infinitezimalnih funkcija.

Razmotrimo neke probleme nalaženja granice u odnosu na prvu izvanrednu granicu; Dajemo detaljan opis rješenja.

Primjer 1

Potrebno je odrediti granicu bez korištenja L'Hopitalovog pravila: lim x → 0 sin (3 x) 2 x .

Rješenje

Zamijenite vrijednost:

lim x → 0 sin (3 x) 2 x = 0 0

Vidimo da postoji nesigurnost oko nule podijeljene sa nulom. Pogledajte tabelu nesigurnosti da navedete metodu rješenja. Kombinacija sinusa i njegovog argumenta daje nam nagoveštaj o upotrebi prve divne granice, ali prvo hajde da transformišemo izraz. Pomnožimo brojilac i imenilac razlomka sa 3 x i dobijemo:

lim x → 0 sin (3 x) 2 x = 0 0 = lim x → 0 3 x sin (3 x) 3 x (2 x) = lim x → 0 sin (3 x) 3 x 3 x 2 x = = lim x → 0 3 2 sin (3 x) 3 x

Na osnovu posledica prvog značajnog ograničenja, imamo: lim x → 0 sin (3 x) 3 x = 1 .

Tada dolazimo do rezultata:

lim x → 0 3 2 sin (3 x) 3 x = 3 2 1 = 3 2

odgovor: lim x → 0 sin (3 x) 3 x = 3 2 .

Primjer 2

Potrebno je pronaći granicu lim x → 0 1 - cos (2 x) 3 x 2 .

Rješenje

Zamijenite vrijednosti i dobijete:

lim x → 0 1 - cos (2 x) 3 x 2 = 1 - cos (2 0) 3 0 2 = 1 - 1 0 = 0 0

Vidimo nesigurnost nule podijeljene sa nulom. Pretvorimo brojilac koristeći trigonometrijske formule:

lim x → 0 1 - cos (2 x) 3 x 2 = 0 0 = lim x → 0 2 sin 2 (x) 3 x 2

Vidimo da je sada moguće primijeniti prvo značajno ograničenje ovdje:

lim x → 0 2 sin 2 (x) 3 x 2 = lim x → 0 2 3 sin x x sin x x = 2 3 1 1 = 2 3

odgovor: lim x → 0 1 - cos (2 x) 3 x 2 = 2 3 .

Primjer 3

Potrebno je izračunati granicu lim x → 0 a r c sin (4 x) 3 x .

Rješenje

Zamijenite vrijednost:

lim x → 0 a r c sin (4 x) 3 x = a r c sin (4 0) 3 0 = 0 0

Vidimo nesigurnost dijeljenja nule sa nulom. Zamenimo:

a r c sin (4 x) = t ⇒ sin (a r c sin (4 x)) = sin (t) 4 x = sin (t) ⇒ x = 1 4 sin (t) lim x → 0 (a r c sin (4 x) ) \u003d a r c sin (4 0) = 0, zatim t → 0 kao x → 0.

U ovom slučaju, nakon promjene varijable, granica poprima oblik:

lim x → 0 a r c sin (4 x) 3 x = 0 0 = lim t → 0 t 3 1 4 sin (t) = = lim t → 0 4 3 t sin t = 4 3 1 = 4 3

odgovor: lim x → 0 a r c sin (4 x) 3 x = 4 3 .

Za potpunije razumijevanje materijala članka potrebno je ponoviti materijal teme „Granice, osnovne definicije, primjeri nalaza, zadaci i rješenja“.

Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter

Formula za drugu izuzetnu granicu je lim x → ∞ 1 + 1 x x = e. Drugi oblik pisanja izgleda ovako: lim x → 0 (1 + x) 1 x = e .

Kada govorimo o drugoj izuzetnoj granici, moramo imati posla sa nesigurnošću oblika 1 ∞ , tj. jedinicu do beskonačnog stepena.

Razmotrimo probleme u kojima nam je potrebna sposobnost izračunavanja druge izuzetne granice.

Primjer 1

Pronađite granični lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 .

Rješenje

Zamijenite željenu formulu i izvršite proračune.

lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = 1 - 2 ∞ 2 + 1 ∞ 2 + 1 4 = 1 - 0 ∞ = 1 ∞

U našem odgovoru, dobili smo jedinicu na moć beskonačnosti. Za određivanje metode rješenja koristimo tablicu nesigurnosti. Biramo drugu izuzetnu granicu i vršimo promjenu varijabli.

t \u003d - x 2 + 1 2 ⇔ x 2 + 1 4 \u003d - t 2

Ako je x → ∞ onda je t → - ∞ .

Da vidimo šta smo dobili nakon zamjene:

lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = 1 ∞ = lim x → ∞ 1 + 1 t - 1 2 t = lim t → ∞ 1 + 1 t t - 1 2 = e - 1 2

odgovor: lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = e - 1 2 .

Primjer 2

Izračunajte granicu lim x → ∞ x - 1 x + 1 x .

Rješenje

Zamijenite beskonačnost i dobijete sljedeće.

lim x → ∞ x - 1 x + 1 x = lim x → ∞ 1 - 1 x 1 + 1 x x = 1 - 0 1 + 0 ∞ = 1 ∞

U odgovoru smo opet dobili isto što i u prethodnom zadatku, dakle, opet možemo koristiti drugu divnu granicu. Zatim moramo odabrati cijeli broj u osnovi funkcije snage:

x - 1 x + 1 = x + 1 - 2 x + 1 = x + 1 x + 1 - 2 x + 1 = 1 - 2 x + 1

Nakon toga, limit poprima sljedeći oblik:

lim x → ∞ x - 1 x + 1 x = 1 ∞ = lim x → ∞ 1 - 2 x + 1 x

Zamjenjujemo varijable. Recimo da je t = - x + 1 2 ⇒ 2 t = - x - 1 ⇒ x = - 2 t - 1 ; ako je x → ∞, tada je t → ∞.

Nakon toga zapisujemo ono što smo dobili u originalnom limitu:

lim x → ∞ x - 1 x + 1 x = 1 ∞ = lim x → ∞ 1 - 2 x + 1 x = lim x → ∞ 1 + 1 t - 2 t - 1 = = lim x → ∞ 1 + 1 t - 2 t 1 + 1 t - 1 = lim x → ∞ 1 + 1 t - 2 t lim x → ∞ 1 + 1 t - 1 = = lim x → ∞ 1 + 1 t t - 2 1 + 1 ∞ = e - 2 (1 + 0) - 1 = e - 2

Da bismo izvršili ovu transformaciju, koristili smo osnovna svojstva granica i moći.

odgovor: lim x → ∞ x - 1 x + 1 x = e - 2 .

Primjer 3

Izračunajte granični lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 .

Rješenje

lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = lim x → ∞ 1 + 1 x 3 1 + 2 x - 1 x 3 3 2 x - 5 x 4 = = 1 + 0 1 + 0 - 0 3 0 - 0 = 1∞

Nakon toga, trebamo izvršiti transformaciju funkcije da primijenimo drugu divnu granicu. dobili smo sljedeće:

lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = 1 ∞ = lim x → ∞ x 3 - 2 x 2 - 1 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5

Pošto sada imamo iste eksponente u brojiocu i nazivniku razlomka (jednaki šest), granica razlomka na beskonačnosti će biti jednaka omjeru ovih koeficijenata na višim potencijama.

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 6 2 = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 3

Zamenivši t = x 2 + 2 x 2 - 1 - 2 x 2 + 2, dobijamo drugu izuzetnu granicu. Znači šta:

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 3 = lim x → ∞ 1 + 1 t t - 3 = e - 3

odgovor: lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = e - 3 .

zaključci

Nesigurnost 1 ∞ , tj. jedinica do beskonačnog stepena, je stepen nesigurnosti, stoga se može otkriti korištenjem pravila za pronalaženje granica eksponencijalnih funkcija stepena.

Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter

Prva izuzetna granica se često koristi za izračunavanje granica koje sadrže sinus, arksinus, tangent, arktangens i rezultirajuće nesigurnosti nulu podijeljenu sa nulom.

Formula

Formula za prvu izuzetnu granicu je: $$ \lim_(\alpha\to 0) \frac(\sin\alpha)(\alpha) = 1 $$

Primjećujemo da $ \alpha\to 0 $ daje $ \sin\alpha \to 0 $, tako da imamo nule u brojiocu i nazivniku. Dakle, formula prve izvanredne granice je potrebna da bi se otkrile nesigurnosti $ \frac(0)(0) $.

Da bi formula mogla da se primeni, moraju biti ispunjena dva uslova:

1. Izrazi sadržani u sinusu i nazivniku razlomka su isti
2. Izrazi u sinusu i nazivniku razlomka teže nuli

Pažnja! $ \lim_(x\to 0) \frac(\sin(2x^2+1))(2x^2+1) \neq 1 $ Iako su izrazi ispod sinusa i u nazivniku isti, ipak $ 2x ^2+1 = 1 $, kada je $ x\ do 0 $. Drugi uslov nije ispunjen, pa se formula NE MOŽE primijeniti!

Posljedice

Vrlo rijetko u zadacima možete vidjeti čistu prvu divnu granicu u koju biste odmah mogli zapisati odgovor. U praksi sve izgleda malo kompliciranije, ali za takve slučajeve bit će korisno znati posljedice prve izvanredne granice. Zahvaljujući njima možete brzo izračunati željene granice.

$$ \lim_(\alpha\to 0) \frac(\alpha)(\sin\alpha) = 1 $$

$$ \lim_(\alpha\to 0) \frac(\sin(a\alpha))(\sin(b\alpha)) = \frac(a)(b) $$

$$ \lim_(\alpha\to 0) \frac(tg\alpha)(\alpha) = 1 $$

$$ \lim_(\alpha\to 0) \frac(\arcsin\alpha)(\alpha) = 1 $$

$$ \lim_(\alpha\to 0) \frac(arctg\alpha)(\alpha) = 1 $$

Primjeri rješenja

Razmotrimo prvu izvanrednu granicu, čiji primjeri rješenja za izračunavanje granica sadrže trigonometrijske funkcije i nesigurnost $ \bigg[\frac(0)(0)\bigg] $

Primjer 1

Izračunajte $ \lim_(x\to 0) \frac(\sin2x)(4x) $

Rješenje

Uzmite u obzir ograničenje i imajte na umu da sadrži sinus. Zatim zamjenjujemo $ x = 0 $ u brojnik i nazivnik i dobijamo nesigurnost nule podijeljenu sa nulom: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \frac(0)( 0) $$ Već su dva znaka da trebate primijeniti divnu granicu, ali postoji mala nijansa: nećemo moći odmah primijeniti formulu, jer se izraz pod znakom sinusa razlikuje od izraza u nazivniku. I trebaju nam da budu ravnopravni. Stoga ćemo ga uz pomoć elementarnih transformacija brojioca pretvoriti u $2x$. Da bismo to učinili, izdvojit ćemo dvojku iz nazivnika razlomka posebnim faktorom. To izgleda ovako: $$ \lim_(x\to 0) \frac(\sin2x)(4x) = \lim_(x\to 0) \frac(\sin2x)(2\cdot 2x) = $$ $$ = \frac(1)(2) \lim_(x\to 0) \frac(\sin2x)(2x) = \frac(1)(2)\cdot 1 = \frac(1)(2) $$ , da je na kraju $ \lim_(x\to 0) \frac(\sin2x)(2x) = 1 $ dobijeno po formuli. Ako ne možete riješiti svoj problem, pošaljite nam ga. Mi ćemo dati detaljno rješenje. Moći ćete se upoznati s napretkom izračunavanja i prikupiti informacije. Ovo će vam pomoći da blagovremeno dobijete kredit od nastavnika!

Odgovori

$$ \lim_(x\to 0) \frac(\sin2x)(4x) =\frac(1)(2) $$

Primjer 2

Pronađite $ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) $

Rješenje

Kao i uvijek, prvo morate znati vrstu neizvjesnosti. Ako je nula podijeljena sa nulom, onda obraćamo pažnju na prisustvo sinusa: $$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = \frac(0) (0) = $$ Ova nesigurnost nam omogućava da koristimo formulu prve izuzetne granice, ali izraz iz nazivnika nije jednak argumentu sinusa? Stoga je nemoguće primijeniti formulu "na čelo". Morate pomnožiti i podijeliti razlomak sa sinusnim argumentom: $$ = \lim_(x\to 0) \frac((x^3+2x)\sin(x^3+2x))((2x-x^) 4)(x ^3+2x)) = $$ Sada opisujemo svojstva granica: $$ = \lim_(x\to 0) \frac((x^3+2x))(2x-x^4 )\cdot \lim_(x \to 0) \frac(\sin(x^3+2x))((x^3+2x)) = $$ Druga granica samo odgovara formuli i jednaka je jedan: $ $ = \lim_(x\to 0 ) \frac(x^3+2x)(2x-x^4)\cdot 1 = \lim_(x\to 0) \frac(x^3+2x)(2x- x^4) = $$ Ponovo zamijenite $ x = 0 $ u razlomak i dobijete nesigurnost $ \frac(0)(0) $. Da biste ga eliminisali, dovoljno je uzeti $ x $ iz zagrada i smanjiti za to: $$ = \lim_(x\to 0) \frac(x(x^2+2))(x(2-x^) 3)) = \ lim_(x\to 0) \frac(x^2+2)(2-x^3) = $$ $$ = \frac(0^2 + 2)(2 - 0^3) = \frac(2)(2) = 1 $$

Odgovori

$$ \lim_(x\to 0) \frac(\sin(x^3+2x))(2x-x^4) = 1 $$

Primjer 4

Izračunajte $ \lim_(x\to0) \frac(\sin2x)(tg3x) $

Rješenje

Započnimo proračun zamjenom $ x=0 $. Kao rezultat, dobijamo nesigurnost $ \frac(0)(0) $. Granica sadrži sinus i tangentu, što nagoveštava mogući razvoj situacije koristeći formulu prve izuzetne granice. Pretvorimo brojilac i imenilac razlomka u formulu i posljedicu: $$ \lim_(x\to0) \frac(\sin2x)(tg3x) = \frac(0)(0) = \lim_(x\to0) \frac(\frac(\sin2x)(2x)\cdot 2x )(\frac(tg3x)(3x)\cdot 3x) = $$ Sada vidimo da u brojniku i nazivniku postoje izrazi pogodni za formulu i posljedice. Argument sinus i argument tangente su isti za odgovarajuće nazivnike $$ = \lim_(x\to0) \frac(1\cdot 2x)(1\cdot 3x) = \frac(2)(3) $$

Odgovori

$$ \lim_(x\to0) \frac(\sin2x)(tg2x) = \frac(2)(3) $$

U članku: "Prva izuzetna granica, primjeri rješenja" rečeno je o slučajevima u kojima je preporučljivo koristiti ovu formulu i njenim posljedicama.