Теперь со спокойной душой переходим к рассмотрению замечательных пределов .
имеет вид .

Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к 0.

Необходимо вычислить предел

Как видно, данный предел очень похож на первый замечательный, но это не совсем так. Вообще, если Вы замечаете в пределе sin, то надо сразу задуматься о том, возможно ли применение первого замечательного предела.

Согласно нашему правилу №1 подставим вместо х ноль:

Получаем неопределенность .

Теперь попробуем самостоятельно организовать первый замечательный предел. Для этого проведем нехитрую комбинацию:

Таким образом мы организовываем числитель и знаменатель так, чтобы выделить 7х. Вот уже и проявился знакомый замечательный предел. Желательно при решении выделять его:

Подставим решение первого замечательного примера и получаем:

Упрощаем дробь:

Ответ: 7/3.

Как видите – все очень просто.

Имеет вид , где e = 2,718281828… – это иррациональное число.

Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к .

Необходимо вычислить предел

Здесь мы видим наличие степени под знаком предела, значит возможно применение второго замечательного предела.

Как всегда воспользуемся правилом №1 – подставим вместо х:

Видно, что при х основание степени , а показатель – 4x > , т.е. получаем неопределенность вида :

Воспользуемся вторым замечательным пределом для раскрытия нашей неопределенности, но сначала надо его организовать. Как видно – надо добиться присутствия в показателе, для чего возведем основание в степень 3х, и одновременно в степень 1/3x, чтобы выражение не менялось:

Не забываем выделять наш замечательный предел:

Вот такие действительно замечательные пределы !
Если у вас остались какие то вопросы по первому и второму замечательным пределам , то смело задавайте их в комментариях.
Всем по возможности ответим.

Также вы можете позаниматься с педагогом по этой теме.
Мы рады предложить вам услуги подбора квалифицированного репетитора в вашем городе. Наши партнеры оперативно подберут для вас хорошего преподавателя на выгодных для вас условиях.

Мало информации? - Вы можете !

Можно писать математические вычисления в блокнотах. В блокноты с логотипом (http://www.blocnot.ru) индивидуальным писать намного приятней.

Замечательных пределов существует несколько, но самыми известными являются первый и второй замечательные пределы. Замечательность этих пределов состоит в том, что они имеют широкое применение и с их помощью можно найти и другие пределы, встречающиеся в многочисленных задачах. Этим мы и будем заниматься в практической части данного урока. Для решения задач путём приведения к первому или второму замечательному пределу не нужно раскрывать содержащиеся в них неопределённости, поскольку значения этих пределов уже давно вывели великие математики.

Первым замечательным пределом называется предел отношения синуса бесконечно малой дуги к той же дуге, выраженной в радианной мере:

Переходим к решению задач на первый замечательный предел. Заметим: если под знаком предела находится тригонометрическая функция, это почти верный признак того, что это выражение можно привести к первому замечательнному пределу.

Пример 1. Найти предел .

Решение. Подстановка вместо x нуля приводит к неопределённости:

.

В знаменателе - синус, следовательно, выражение можно привести к первому замечательному пределу. Начинаем преобразования:

.

В знаменателе - синус трёх икс, а в числителе всего лишь один икс, значит, нужно получить три икс и в числителе. Для чего? Чтобы представить 3x = a и получить выражение .

И приходим к разновидности первого замечательного предела:

потому что неважно, какая буква (переменная) в этой формуле стоит вместо икса.

Умножаем икс на три и тут же делим:

.

В соответствии с замеченным первым замечательным пределом производим замену дробного выражения:

Теперь можем окончательно решить данный предел:

.

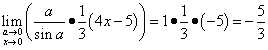Пример 2. Найти предел .

Решение. Непосредственная подстановка вновь приводит к неопределённости "нуль делить на нуль":

.

Чтобы получить первый замечательный предел, нужно, чтобы икс под знаком синуса в числителе и просто икс в знаменателе были с одним и тем же коэффициентом. Пусть этот коэффициент будет равен 2. Для этого представим нынешний коэффициент при иксе как и далее, производя действия с дробями, получаем:

.

Пример 3. Найти предел .

Решение. При подстановке вновь получаем неопределённость "нуль делить на нуль":

.

Наверное, вам уже понятно, что из исходного выражения можно получить первый замечательный предел, умноженный на первый замечательный предел. Для этого раскладываем квадраты икса в числителе и синуса в знаменателе на одинаковые множители, а чтобы получить у иксов и у синуса одинаковые коэффициенты, иксы в числителе делим на 3 и тут же умножаем на 3. Получаем:

.

Пример 4. Найти предел .

Решение. Вновь получаем неопределённость "нуль делить на нуль":

.

Можем получить отношение двух первых замечательных пределов. Делим и числитель, и знаменатель на икс. Затем, чтобы коэффициенты при синусах и при иксах совпадали, верхний икс умножаем на 2 и тут же делим на 2, а нижний икс умножаем на 3 и тут же делим на 3. Получаем:

Пример 5. Найти предел .

Решение. И вновь неопределённость "нуль делить на нуль":

Помним из тригонометрии, что тангенс - это отношение синуса к косинусу, а косинус нуля равен единице. Производим преобразования и получаем:

.

Пример 6. Найти предел .

Решение. Тригонометрическая функция под знаком предела вновь наталкивает на мысль о применении первого замечательного предела. Представляем его как отношение синуса к косинусу.

Первый замечательный предел выглядит следующим образом: lim x → 0 sin x x = 1 .

В практических примерах часто встречаются модификации первого замечательного предела: lim x → 0 sin k · x k · x = 1 , где k – некоторый коэффициент.

Поясним: lim x → 0 sin (k · x) k · x = п у с т ь t = k · x и з x → 0 с л е д у е т t → 0 = lim t → 0 sin (t) t = 1 .

Следствия первого замечательного предела:

1. lim x → 0 x sin x = lim x → 0 = 1 sin x x = 1 1 = 1

1. lim x → 0 k · x sin k · x = lim x → 0 1 sin (k · x) k · x = 1 1 = 1

Указанные следствия достаточно легко доказать, применив правило Лопиталя или замену бесконечно малых функций.

Рассмотрим некоторые задачи на нахождение предела по первому замечательному пределу; дадим подробное описание решения.

Пример 1

Необходимо определить предел, не используя правило Лопиталя: lim x → 0 sin (3 x) 2 x .

Решение

Подставим значение:

lim x → 0 sin (3 x) 2 x = 0 0

Мы видим, что возникла неопределенность нуль делить на нуль. Обратимся к таблице неопределенностей, чтобы задать метод решения. Сочетание синуса и его аргумента дает нам подсказку об использовании первого замечательного предела, однако для начала преобразуем выражение. Произведем умножение числителя и знаменателя дроби на 3 x и получим:

lim x → 0 sin (3 x) 2 x = 0 0 = lim x → 0 3 x · sin (3 x) 3 x · (2 x) = lim x → 0 sin (3 x) 3 x · 3 x 2 x = = lim x → 0 3 2 · sin (3 x) 3 x

Опираясь на следствие из первого замечательного предела, имеем: lim x → 0 sin (3 x) 3 x = 1 .

Тогда приходим к результату:

lim x → 0 3 2 · sin (3 x) 3 x = 3 2 · 1 = 3 2

Ответ: lim x → 0 sin (3 x) 3 x = 3 2 .

Пример 2

Необходимо найти предел lim x → 0 1 - cos (2 x) 3 x 2 .

Решение

Подставим значения и получим:

lim x → 0 1 - cos (2 x) 3 x 2 = 1 - cos (2 · 0) 3 · 0 2 = 1 - 1 0 = 0 0

Мы видим неопределенность нуль делить на нуль. Произведем преобразование числителя с использованием формул тригонометрии:

lim x → 0 1 - cos (2 x) 3 x 2 = 0 0 = lim x → 0 2 sin 2 (x) 3 x 2

Видим, что теперь здесь возможно применение первого замечательного предела:

lim x → 0 2 sin 2 (x) 3 x 2 = lim x → 0 2 3 · sin x x · sin x x = 2 3 · 1 · 1 = 2 3

Ответ: lim x → 0 1 - cos (2 x) 3 x 2 = 2 3 .

Пример 3

Необходимо произвести вычисление предела lim x → 0 a r c sin (4 x) 3 x .

Решение

Подставим значение:

lim x → 0 a r c sin (4 x) 3 x = a r c sin (4 · 0) 3 · 0 = 0 0

Мы видим неопределенность делить нуль на нуль. Произведем замену:

a r c sin (4 x) = t ⇒ sin (a r c sin (4 x)) = sin (t) 4 x = sin (t) ⇒ x = 1 4 sin (t) lim x → 0 (a r c sin (4 x)) = a r c sin (4 · 0) = 0 , значит t → 0 при x → 0 .

В таком случае, после замены переменной, предел принимает вид:

lim x → 0 a r c sin (4 x) 3 x = 0 0 = lim t → 0 t 3 · 1 4 sin (t) = = lim t → 0 4 3 · t sin t = 4 3 · 1 = 4 3

Ответ: lim x → 0 a r c sin (4 x) 3 x = 4 3 .

Для более полного понимания материала статьи следует повторить материал темы «Пределы, основные определения, примеры нахождения, задачи и решения».

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Формула второго замечательного предела имеет вид lim x → ∞ 1 + 1 x x = e . Другая форма записи выглядит так: lim x → 0 (1 + x) 1 x = e .

Когда мы говорим о втором замечательном пределе, то нам приходится иметь дело с неопределенностью вида 1 ∞ , т.е. единицей в бесконечной степени.

Рассмотрим задачи, в которых нам пригодится умение вычислять второй замечательный предел.

Пример 1

Найдите предел lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 .

Решение

Подставим нужную формулу и выполним вычисления.

lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = 1 - 2 ∞ 2 + 1 ∞ 2 + 1 4 = 1 - 0 ∞ = 1 ∞

У нас в ответе получилась единица в степени бесконечность. Чтобы определиться с методом решения, используем таблицу неопределенностей. Выберем второй замечательный предел и произведем замену переменных.

t = - x 2 + 1 2 ⇔ x 2 + 1 4 = - t 2

Если x → ∞ , тогда t → - ∞ .

Посмотрим, что у нас получилось после замены:

lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = 1 ∞ = lim x → ∞ 1 + 1 t - 1 2 t = lim t → ∞ 1 + 1 t t - 1 2 = e - 1 2

Ответ: lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = e - 1 2 .

Пример 2

Вычислите предел lim x → ∞ x - 1 x + 1 x .

Решение

Подставим бесконечность и получим следующее.

lim x → ∞ x - 1 x + 1 x = lim x → ∞ 1 - 1 x 1 + 1 x x = 1 - 0 1 + 0 ∞ = 1 ∞

В ответе у нас опять получилось то же самое, что и в предыдущей задаче, следовательно, мы можем опять воспользоваться вторым замечательным пределом. Далее нам нужно выделить в основании степенной функции целую часть:

x - 1 x + 1 = x + 1 - 2 x + 1 = x + 1 x + 1 - 2 x + 1 = 1 - 2 x + 1

После этого предел приобретает следующий вид:

lim x → ∞ x - 1 x + 1 x = 1 ∞ = lim x → ∞ 1 - 2 x + 1 x

Заменяем переменные. Допустим, что t = - x + 1 2 ⇒ 2 t = - x - 1 ⇒ x = - 2 t - 1 ; если x → ∞ , то t → ∞ .

После этого записываем, что у нас получилось в исходном пределе:

lim x → ∞ x - 1 x + 1 x = 1 ∞ = lim x → ∞ 1 - 2 x + 1 x = lim x → ∞ 1 + 1 t - 2 t - 1 = = lim x → ∞ 1 + 1 t - 2 t · 1 + 1 t - 1 = lim x → ∞ 1 + 1 t - 2 t · lim x → ∞ 1 + 1 t - 1 = = lim x → ∞ 1 + 1 t t - 2 · 1 + 1 ∞ = e - 2 · (1 + 0) - 1 = e - 2

Чтобы выполнить данное преобразование, мы использовали основные свойства пределов и степеней.

Ответ: lim x → ∞ x - 1 x + 1 x = e - 2 .

Пример 3

Вычислите предел lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 .

Решение

lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = lim x → ∞ 1 + 1 x 3 1 + 2 x - 1 x 3 3 2 x - 5 x 4 = = 1 + 0 1 + 0 - 0 3 0 - 0 = 1 ∞

После этого нам нужно выполнить преобразование функции для применения второго замечательного предела. У нас получилось следующее:

lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = 1 ∞ = lim x → ∞ x 3 - 2 x 2 - 1 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5

Поскольку сейчас у нас есть одинаковые показатели степени в числителе и знаменателе дроби (равные шести), то предел дроби на бесконечности будет равен отношению данных коэффициентов при старших степенях.

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 6 2 = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 3

При замене t = x 2 + 2 x 2 - 1 - 2 x 2 + 2 у нас получится второй замечательный предел. Значит, что:

lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 3 = lim x → ∞ 1 + 1 t t - 3 = e - 3

Ответ: lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = e - 3 .

Выводы

Неопределенность 1 ∞ , т.е. единица в бесконечной степени, является степенной неопределенностью, следовательно, ее можно раскрыть, используя правила нахождения пределов показательно степенных функций.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Первый замечательный предел часто применяется для вычисления пределов содержащих синус, арксинус, тангенс, арктангенс и получающихся при них неопределенностей ноль делить на ноль.

Формула

Формула первого замечательного предела имеет вид: $$ \lim_{\alpha\to 0} \frac{\sin\alpha}{\alpha} = 1 $$

Замечаем, что при $ \alpha\to 0 $ получается $ \sin\alpha \to 0 $, тем самым в числетеле и в знаменателе имеем нули. Таким образом формула первого замечательного предела нужна для раскрытия неопределенностей $ \frac{0}{0} $.

Для применения формулы необходимо, чтобы были соблюдены два условия:

1. Выражения, содержащиеся в синусе и знаменателе дроби совпадают
2. Выражения, стоящие в синусе и знаменателе дроби стремятся к нулю

Внимание! $ \lim_{x\to 0} \frac{\sin(2x^2+1)}{2x^2+1} \neq 1 $ Хотя выражения под синусом и в знаменателе одинаковые, однако $ 2x^2+1 = 1 $, при $ x\to 0 $. Не выполнено второе условие, поэтому применять формулу НЕЛЬЗЯ!

Следствия

Достаточно редко в задания можно увидеть чистый первый замечательный предел, в котором можно сразу было бы записать ответ. На практике всё немного сложнее выглядит, но для таких случаев будет полезно знать следствия первого замечательного предела. Благодаря им можно быстро вычислить нужные пределы.

$$ \lim_{\alpha\to 0} \frac{\alpha}{\sin\alpha} = 1 $$

$$ \lim_{\alpha\to 0} \frac{\sin(a\alpha)}{\sin(b\alpha)} = \frac{a}{b} $$

$$ \lim_{\alpha\to 0} \frac{tg\alpha}{\alpha} = 1 $$

$$ \lim_{\alpha\to 0} \frac{\arcsin\alpha}{\alpha} = 1 $$

$$ \lim_{\alpha\to 0} \frac{arctg\alpha}{\alpha} = 1 $$

Примеры решений

Рассмотрим первый замечательный предел, примеры решения которого на вычисление пределов содержащих тригонометрические функции и неопределенность $ \bigg[\frac{0}{0}\bigg] $

Пример 1

Вычислить $ \lim_{x\to 0} \frac{\sin2x}{4x} $

Решение

Рассмотрим предел и заметим, что в нём присутствует синус. Далее подставим $ x = 0 $ в числитель и знаменатель и получим неопределенность нуль делить на нуль: $$ \lim_{x\to 0} \frac{\sin2x}{4x} = \frac{0}{0} $$ Уже два признака того, что нужно применять замечательный предел, но есть небольшой нюанс: сразу применить формулу мы не сможем, так как выражение под знаком синуса отличается от выражения стоящего в знаменателе. А нам нужно, чтобы они были равны. Поэтому с помощью элементарных преобразований числителя мы превратим его в $ 2x $. Для этого мы вынесем двойку из знаменателя дроби отдельным множителем. Выглядит это так: $$ \lim_{x\to 0} \frac{\sin2x}{4x} = \lim_{x\to 0} \frac{\sin2x}{2\cdot 2x} = $$ $$ = \frac{1}{2} \lim_{x\to 0} \frac{\sin2x}{2x} = \frac{1}{2}\cdot 1 = \frac{1}{2} $$ Обратите внимание, что в конце $ \lim_{x\to 0} \frac{\sin2x}{2x} = 1 $ получилось по формуле. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ \lim_{x\to 0} \frac{\sin2x}{4x} =\frac{1}{2} $$

Пример 2

Найти $ \lim_{x\to 0} \frac{\sin(x^3+2x)}{2x-x^4} $

Решение

Как всегда сначала нужно узнать тип неопределенности. Если она нуль делить на нуль, то обращаем внимание на наличие синуса: $$ \lim_{x\to 0} \frac{\sin(x^3+2x)}{2x-x^4} = \frac{0}{0} = $$ Данная неопределенность позволяет воспользоваться формулой первого замечательного предела, но выражение из знаменателя не равно аргументу синуса? Поэтом "в лоб" применить формулу нельзя. Необходимо умножить и разделить дробь на аргумент синуса: $$ = \lim_{x\to 0} \frac{(x^3+2x)\sin(x^3+2x)}{(2x-x^4)(x^3+2x)} = $$ Теперь по свойствам пределов расписываем: $$ = \lim_{x\to 0} \frac{(x^3+2x)}{2x-x^4}\cdot \lim_{x\to 0} \frac{\sin(x^3+2x)}{(x^3+2x)} = $$ Второй предел как раз подходит под формулу и равен единице: $$ = \lim_{x\to 0} \frac{x^3+2x}{2x-x^4}\cdot 1 = \lim_{x\to 0} \frac{x^3+2x}{2x-x^4} = $$ Снова подставляем $ x = 0 $ в дробь и получаем неопределенность $ \frac{0}{0} $. Для её устранения достоточно вынести за скобки $ x $ и сократить на него: $$ = \lim_{x\to 0} \frac{x(x^2+2)}{x(2-x^3)} = \lim_{x\to 0} \frac{x^2+2}{2-x^3} = $$ $$ = \frac{0^2 + 2}{2 - 0^3} = \frac{2}{2} = 1 $$

Ответ

$$ \lim_{x\to 0} \frac{\sin(x^3+2x)}{2x-x^4} = 1 $$

Пример 4

Вычислить $ \lim_{x\to0} \frac{\sin2x}{tg3x} $

Решение

Вычисление начнём с подстановки $ x=0 $. В результате получаем неопределенность $ \frac{0}{0} $. Предел содержит синус и тангенс, что намекает на возможное развитие ситуации с использованием формулы первого замечательного предела. Преобразуем числитель и знаменатель дроби под формулу и следствие: $$ \lim_{x\to0} \frac{\sin2x}{tg3x} = \frac{0}{0} = \lim_{x\to0} \frac{\frac{\sin2x}{2x}\cdot 2x}{\frac{tg3x}{3x}\cdot 3x} = $$ Теперь видим в числителе и знаменателе появились выражения подходящие под формулу и следствия. Аргумент синуса и аргумент тангенса совпадают для соответствующих знаменателей $$ = \lim_{x\to0} \frac{1\cdot 2x}{1\cdot 3x} = \frac{2}{3} $$

Ответ

$$ \lim_{x\to0} \frac{\sin2x}{tg2x} = \frac{2}{3} $$

В статье: "Первый замечательный предел, примеры решения" было рассказано о случаях, в которых целесообразно использовать данную формулу и её следствия.